Complex numbers (HL)

Two-dimensional numbers

Loosely speaking, complex numbers are two-dimensional numbers for which arithmetic operations are defined. Various connections to two-dimensional vectors and trigonometry will be pointed out, where they arise.

Contents

Imaginary unit and Argand diagram

i=−1\i = \sqrt{-1}

This is hardly a definition, since the square root is doing most of the heavy-lifting. Just like 33 and −3-3 are solutions to x2=9x^2 = 9, i\i and −i-\i are solutions to x2=−1x^2 = -1.

Examples of complex numbers include 3−2i3 - 2\i, −4.83+i3-4.83 + \i\sqrt{3}, 5i5\i and 57\frac{5}{7}.

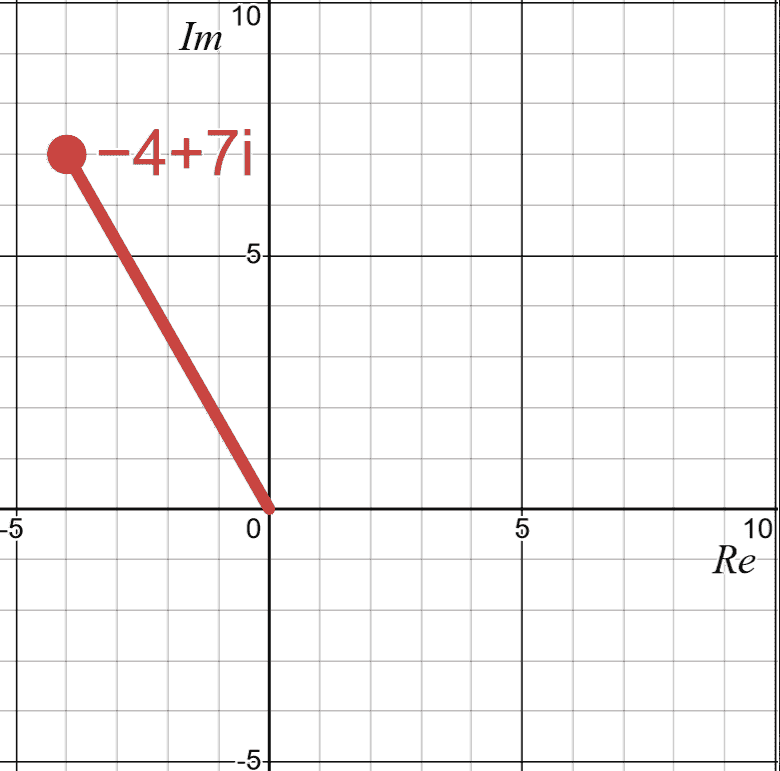
−4 + 7i on Argand diagram is like the point (−4, 7) on Cartesian coordinates
The complex number −4 + 7i

Intuitively, i\i is like the yy on the xyxy-plane. The Argand diagram is very similar to the xyxy-plane itself, with real axis Rez\text{Re}z perpendicular to the imaginary axis Imz\text{Im}z. Each point on the real-imaginary plane represents a single complex number.

Definitions

purely imaginary number is a complex number with no real part, such as −3i-3\i.

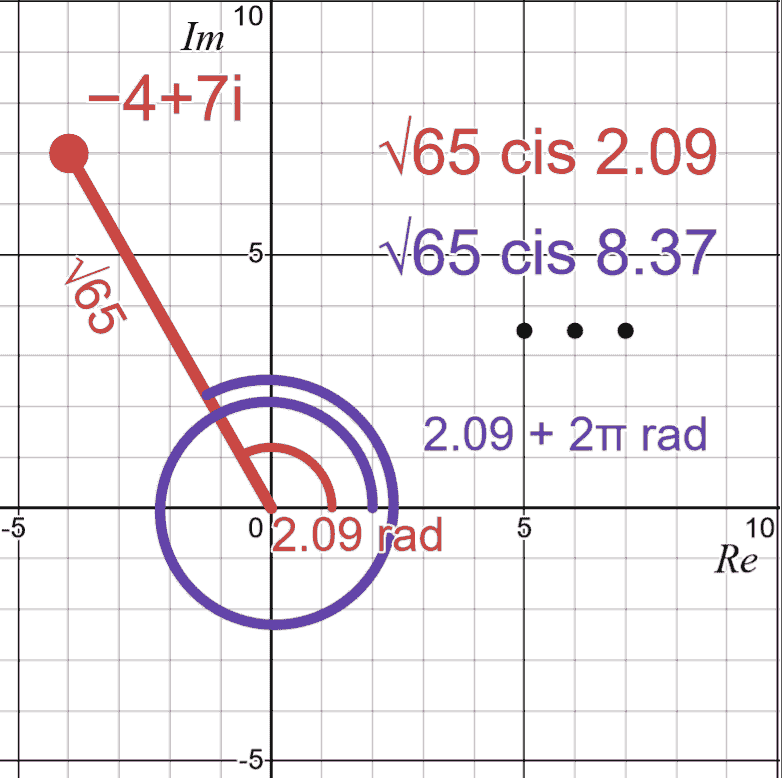
modulus, or ∣z∣\lvert z\rvert, or rr, is the distance between a complex number and 0, on the Argand diagram. This applies the distance formula analogous to the magnitude of a vector.

argument, argz\text{arg}z is the counterclockwise (anticlockwise) angle (usually in radians) that the number makes with the real axis. Historically, IB accepted either a range of argz∈]−π,π]\text{arg}z \in \left]-\pi, \pi\right] or argz∈[0,2π[\text{arg}z \in \left[0, 2\pi\right[. In contrast, θ\theta may refer to any of the infinite arguments off by 2π2\pi radians.

−4 + 7i showing modulus as a length and argument as the angle counterclockwise from the real axis
−4 + 7i in two of an infinite number of polar forms, each with argument 2π radians apart

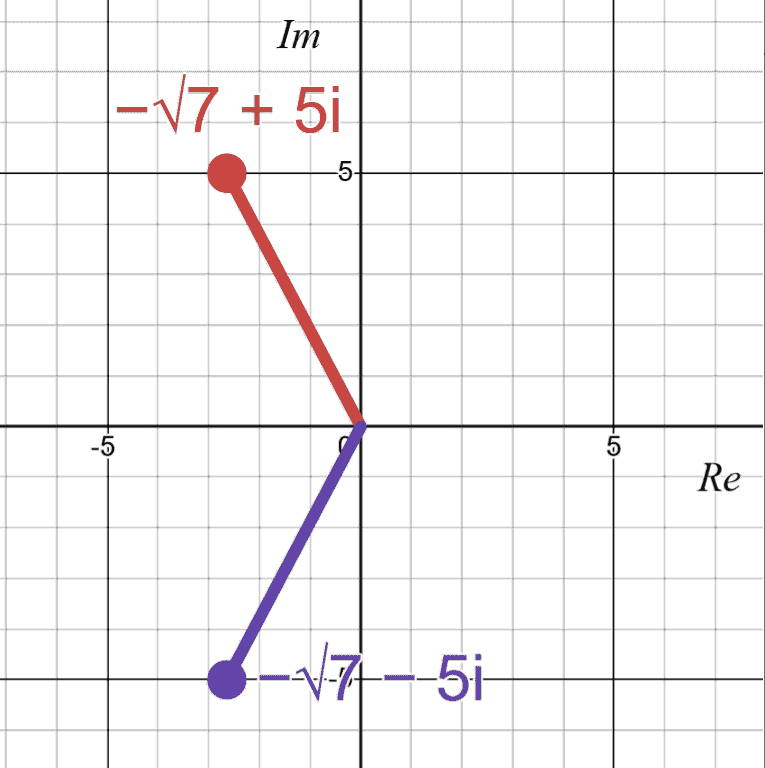
complex conjugate, or z∗z^*, or zˉ\bar z, is the complex number with the same real part as zz, but the imaginary part of zz differ by a negative sign.

−√7 + 5i and −√7 − 5i on Argand diagram
−√7 + 5i and −√7 − 5i are complex conjugates of each other.

Notations

Rectangular (Cartesian) form a+bia + b\i

modulus-argument (polar) form r(cos⁡θ+isin⁡θ)r(\cos\theta + \i\sin\theta) or r cis θr\cis\theta

exponential (Euler) form r eiθr\,\e^{\i\theta}

In particular the same complex number can have multiple polar/Euler forms, but only one Cartesian form. That is,

a+bi=c+di  ⟺  a=c,  b=da + b\i = c + d\i \iff a = c,\;b = d

For the rest of the page, “polar” refers to both polar and Euler forms.

Converting from r cis θr\cis\theta to a+bia+b\i

a=rcos⁡θa = r\cos\theta
b=rsin⁡θb = r\sin\theta

Converting from a+bia + b\i to r cis θr\cis\theta

There is only one modulus

r=a2+b2r = \sqrt{a^2 + b^2}

but possibly multiple arguments. The most common range of argz∈]−π,π]\text{arg}z \in \left]-\pi, \pi\right], though the alternative range argz∈[0,2π[\text{arg}z \in \left[0, 2\pi\right[ has also been used or accepted on exams.

We will look at the four quadrants separately, then summarize at the end. They all involve arctan⁡ba\arctan \frac{b}{a}. The range of arctan⁡\arctan is ]−π2,π2[{\left]-\frac\pi2, \frac\pi2\right[}.

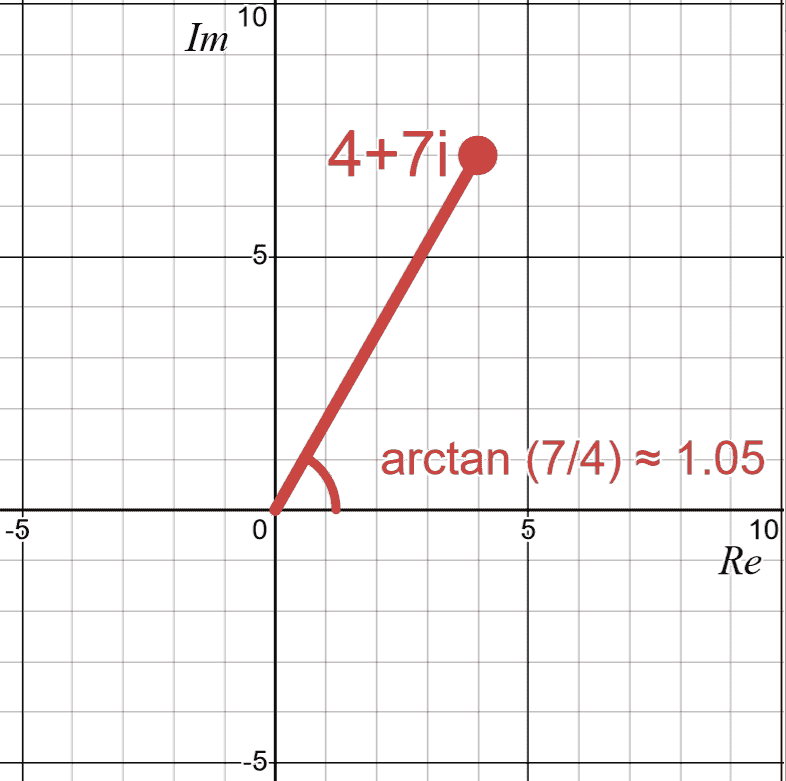
positive real and imaginary is a simple arctan
Quadrant 1 is a simple arctan
positive real and negative imaginary is a simple arctan, or if necessary add by 2 pi
Quadrant 4 is a simple arctan, or if it needs to be positive, then add 2π
negative real and positive imaginary is arctan then add pi
Quadrant 2 is arctan, but add π
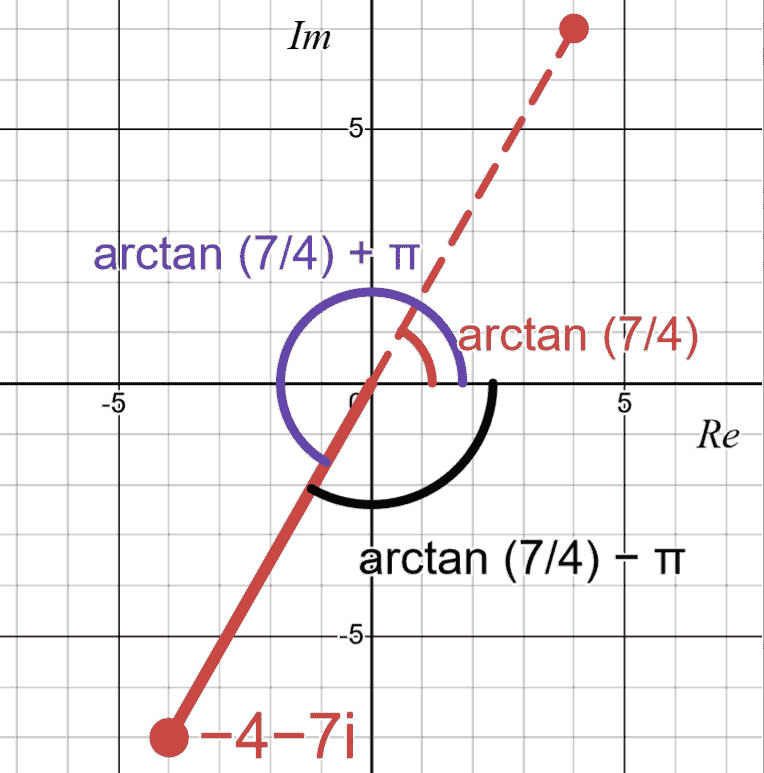
negative real and imaginary is arctan then add or subtract pi, depending on the desired interval
Quadrant 3 is arctan but add π if you want positive argument, or subtract π if you want argument between -π and +π

The predominant definition of arg\text{arg} in argz∈]−π,π]\text{arg}z \in \left]-\pi, \pi\right] involves

argz={undefinedif z=0π2if a=0,b>0−π2if a=0,b<0arctan⁡baif a>0arctan⁡ba+πif a<0,b≥0arctan⁡ba−πif a<0,b<0\text{arg} z= \begin{cases} \text{undefined} & \text{if } z = 0 \\ \frac{\pi}{2} & \text{if } a = 0, b > 0 \\ -\frac{\pi}{2} & \text{if }a = 0, b < 0 \\ \arctan{\frac ba}&\text{if }a > 0 \\ \arctan{\frac ba} + \pi &\text{if }a < 0, b \geq 0 \\ \arctan{\frac ba} - \pi &\text{if }a < 0, b < 0 \end{cases}

This is sometimes known as the atan2\text{atan2} function. Some authors define arg(0)=0\text{arg}(0) = 0 and some leave it undefined. The latter definition is more consistent with complex numbers multiplication and 000^0 as an indeterminate form.

In certain cases where IB requires the argument to be positive,

θ={undefinedif z=0π2if a=0,b>0−π2if a=0,b<0arctan⁡baif a>0,b≥0arctan⁡ba+2πif a>0,b<0arctan⁡ba+πif a<0\theta = \begin{cases} \text{undefined} & \text{if } z = 0 \\ \frac{\pi}{2} & \text{if } a = 0, b > 0 \\ -\frac{\pi}{2} & \text{if }a = 0, b < 0 \\ \arctan{\frac ba} & \text{if }a > 0, b \geq 0 \\ \arctan{\frac ba} + 2\pi & \text{if }a > 0, b < 0 \\ \arctan{\frac ba} + \pi &\text{if }a < 0 \end{cases}

which is simply the prevalent definition of arg\text{arg} but adding 2π2\pi whenever it is negative.

Example: Convert −14+34i-\frac{1}{4} + \frac{3}{4} \i to polar form.

The complex number can be written as 14(−1+3i){\frac14(-1 + 3\i)}, so the modulus is 14\frac14 times modulus of −1+3i{-1 + 3\i}.

r=14((−1)2+32)=104r = \frac{1}{4} \left(\sqrt{(-1)^2 + 3^2}\right) = \frac{\sqrt{10}}{4}

Because a<0,  b≥0a < 0,\; b\geq0, we add π\pi radians to the arctan⁡\arctan.

θ=arctan⁡3−1+π=arctan⁡(−3)+π=π−arctan⁡3\begin{align*} \theta &= \arctan{\frac{3}{-1}} + \pi \\ &= \arctan (-3) + \pi \\ &= \pi - \arctan 3\end{align*}

which uses arctan⁡(−x)=−arctan⁡x\arctan (-x) = -\arctan x, as arctan⁡\arctan is an odd function.

The complex number in polar form is 104 cis (π−arctan⁡3)■{\frac{\sqrt{10}}{4} \cis (\pi - \arctan 3)} \qed

Arithmetics

operationrectangularpolar
addition(a+bi)+(c+di)=a+c+(b+d)i(a+b\i) + (c+d\i) = a + c + (b+d)\ir1 cis θ+r2 cis ϕ=(r1cos⁡θ+r2cos⁡ϕ)+i(r1sin⁡θ+r2sin⁡ϕ)r_1\cis\theta + r_2\cis\phi = (r_1\cos\theta + r_2\cos\phi) + i(r_1\sin\theta + r_2\sin\phi)
subtraction(a+bi)−(c+di)=a−c+(b−d)i(a+b\i) - (c+d\i) = a - c + (b-d)\ir1 cis θ−r2 cis ϕ=(r1cos⁡θ−r2cos⁡ϕ)+i(r1sin⁡θ−r2sin⁡ϕ)r_1\cis\theta - r_2\cis\phi = (r_1\cos\theta - r_2\cos\phi) + i(r_1\sin\theta - r_2\sin\phi)
multiplication(a+bi)(c+di)=ac−bd+i(bc+ad)(a + b\i)(c + d\i) = ac - bd + \i(bc + ad)r1 cis θ⋅r2 cis ϕ=r1r2 cis (θ+ϕ)r_1\cis\theta \cdot r_2\cis\phi = r_1r_2\, \text{cis}\,(\theta+\phi)
divisiona+bic+di=ac+bd+i(bc−ad)c2+d2\displaystyle \frac{a + b\i}{c + d\i} = \frac{ac + bd + \i(bc - ad)}{c^2+d^2}r1 cis θr2 cis ϕ=r1r2 cis (θ−ϕ)\displaystyle \frac{r_1\cis\theta}{r_2\cis\phi} = \frac{r_1}{r_2}\, \text{cis}\,({\theta-\phi})
exponentiation(a+bi)n=∑r=0n(nr)an−r(bi)r(binomial theorem)\displaystyle(a + b\i)^n = \sum_{r=0}^n \binom nr a^{n-r}(b\i)^r \\ \text{(binomial theorem)}(r cis θ)n=rn cis (nθ)(de Moivre’s theorem)\displaystyle(r\cis\theta)^n = r^n\cis(n\theta) \\ \text{(de Moivre's theorem)}

In summary, addition and subtraction are easier in rectangular form, whereas multiplication, division, and exponentiation are easier in polar form.

Example: Simplify 3−i−2+3i\displaystyle \frac{3 - \i}{-2 + 3\i}.

Multiply top and bottom by the complex conjugate of the bottom.

3−i−2+3i=(3−i)(−2−3i)(−2+3i)(−2−3i)=−6−3+2i−9i4+9=−9−7i13■\begin{align*} \frac{3 - \i}{-2 + 3\i} &= \frac{(3-\i)(-2 - 3\i)}{(-2 + 3\i)(-2 - 3\i)} \\ &= \frac{-6 - 3 +2\i - 9\i}{4 + 9} \\ &= \frac{-9 - 7\i}{13} \qed \end{align*}

Complex number addition and subtraction are analogous to their counterparts in vectors..

Multiplying a complex number by a real number kk means keeping the argument, but multiplying the modulus by kk. This is akin to scalar multiplication of vectors.

Multiplying two complex numbers result in a complex number whose modulus is product of the two moduli and argument is sum of the two arguments (perhaps off by 2kπ2k\pi radians).

Properties

Most properties of real numbers apply to complex numbers. A notable exception is complex numbers to the power of complex numbers (beyond syllabus). In addition, fractional exponents are allowed (see section below) as long as a particular value is chosen as the principal value.

Example: Evaluate 5−2+3i5^{-2 + 3\i}.

5−2+3i=5−2⋅e3iln⁡5=125⋅ei⋅3ln⁡5■\begin{align*} 5^{-2 + 3\i} &= 5^{-2}\cdot \e^{3\i\ln5} \\ &= \frac{1}{25} \cdot \e^{\i \cdot 3\ln5} \qed \\ \end{align*}

From calculator we see 3π2<3ln⁡5<2π\displaystyle \frac{3\pi}{2} < 3\ln5 < 2\pi, so the real part is positive, and imaginary part is negative.

Note: 5x5^x and other exponential functions have multiple branches when x∈Cx \in \mathbb{C}. Here we were using the principal branch.

Important properties are as follows. ww and zz are complex numbers. nn is any integer.

i0=i4n=1i1=i4n+1=ii2=i4n+2=−1i3=i4n+3=−i\begin{align*} \i^0 = \i^{4n} &= 1 \\ \i^1 = \i^{4n+1} &= \i \\ \i^2 = \i^{4n+2} &= -1 \\ \i^3 = \i^{4n+3} &= -\i \end{align*}

Multiplication of complex numbers:

eiθeiϕ=ei(θ+ϕ)\e^{\i\theta}\e^{\i\phi} = \e^{\i(\theta+\phi)}
1w=w−1\frac 1w = w^{-1}

Properties of complex numbers can be derived from the above extensions of arithmetics into complex numbers.

Properties from rectangular form addition and subtraction include

z+z∗=2Rezz + z^* = 2\text{Re}z
z−z∗=2Imzz - z^* = 2\text{Im}z

Properties involving modulus include

∣z∗∣=∣z∣\lvert z^*\rvert = \lvert z\rvert
zz∗=∣z∣2zz^* = \lvert z\rvert^2

Tip: When multiplying or adding a complex number and its complex conjugate, the imaginary parts cancel. The difference is that in addition we get twice the real part, while in multiplication we get square of the modulus.

Properties involving polar form multiplication, division, and exponentiation include

∣wz∣=∣w∣∣z∣\lvert wz\rvert = \lvert w\rvert\lvert z\rvert
∣zn∣=∣z∣n,  n∈Z+\lvert z^n\rvert = \lvert z\rvert^n,\; n \in \mathbb Z^+

Fractional exponents of complex numbers

Recall

xmn=xmn=(xn)m\large x^\frac{m}{n} = \sqrt[n]{x^m} = (\sqrt[n]{x})^m

Back in good old days of real numbers, we chose 9\sqrt{9} to mean 33, and not −3-3. We can extend the zn\sqrt[n]{z} for complex numbers by saying the principal root of zz with the least positive argument.

For example, the principal value of −273\sqrt[3]{-27} is 3 cis π3{3 \cis \frac{\pi}{3}}, but the real value is −3-3. This leads to ambiguity in the mathematical notation.

In general, questions typically will say solve x5=r cis θx^5 = r\cis\theta, rather than finding r cis θ5\sqrt[5]{r\cis\theta}.

The nn solutions to (r cis θ)n,n∈Z+(r\cis\theta)^n, n\in\mathbb{Z}^+, using de Moivre’s theorem, are

r1n cis θ+2kπn,    k=0,1,…,n−1r^\frac{1}{n}\cis\frac{\theta+2k\pi}{n}, \;\; k = 0, 1, \dots, n-1
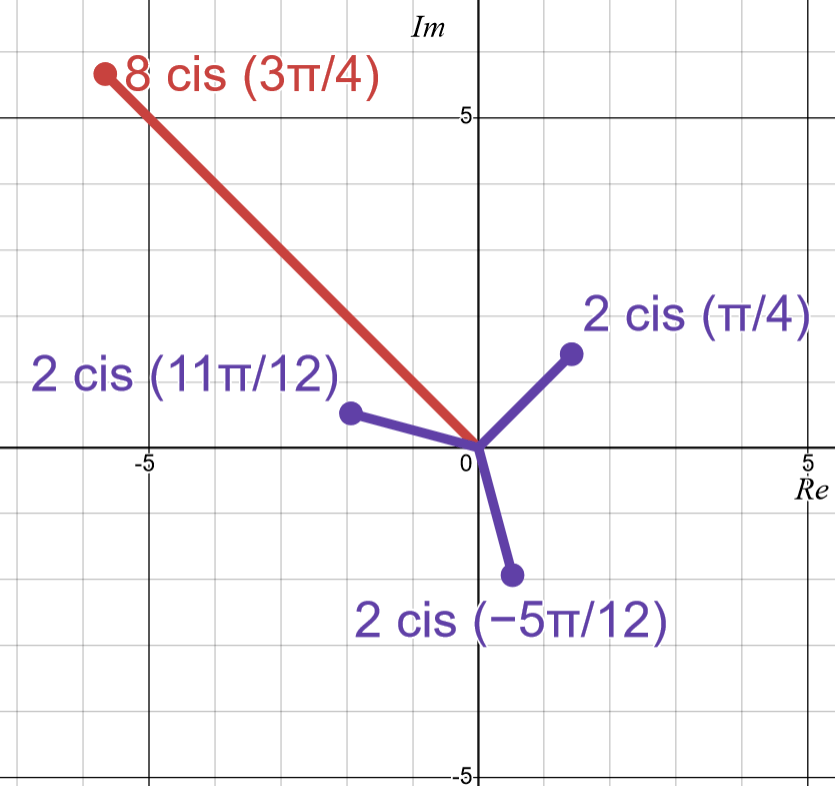
Showing cube roots of 8 cis (3π/4) are equally spaced radially.
Solutions to z³ = 8 cis (3π/4) are z = 2 cis (π/4), 2 cis (11π/12), 2 cis (19π/12) (or 2 cis (−5π/12))

In particular, r1nr^\frac 1n is always a positive real number, and each solution is 2πn\frac{2\pi}{n} apart. So on the Argand diagram, all solutions have the same modulus, and are equally spaced with an angle 2πn\frac{2\pi}{n} in between the solutions.

Real polynomials

For a real polynomial, ie a polynomial with only real coefficients, if a+bia + b\i is a root, then so is a−bia - b\i.

Fundamental theorem of algebra

See also fundamental theorem of algebra and multiplicity

The fundamental theorem of algebra states that a degree-nn polynomial has exactly nn roots, though some of them may be repeated roots.

In particular, depending on the discriminant (Δ\Delta), a quadratic has either two different real roots, two repeated real roots, or two roots that are complex conjugates of each other. All three cases can be solved using the quadratic formula.

Note: The fundamental theorem of algebra does not apply if a complex conjugate is involved in the equation itself.

In cases of working with polar form and the fundamental theorem of algebra, remember that there are an infinite number of arguments for each complex root. In other words, the fundamental theorem of algebra does not apply to arguments, rather only to the complex roots themselves.

Complex numbers and trig proofs

Expansion is possible via both binomial theorem and de Moivre’s theorem (in rectangular and polar forms). Questions often involve comparing coefficients using the two expansions.

Typically, this also involves expressing trig functions all in terms of complex numbers, or vice versa.