Inverse of invertible functions

The inverse function of $f$ is denoted by $f^{-1}$.

Not to be confused with reciprocal functions $f(x)^{-1}$ in HL.

When we are solving for $x$ in an equation, we are really finding the inverse function.

Contents

• Properties
• Calculating the inverse function
• Calculator

Properties

The defining property of an inverse function:

An invertible function $f$ satisfies

The domain of $f^{-1}$ is the range of $f$; the range of $f^{-1}$ is the domain of $f$. You can use this without finding the inverse.

The inverse function is the mirror image of the invertible function across the diagonal line $y = x$.

An invertible function and its inverse can only meet on the $y = x$ diagonal line.

The inverse is also invertible, such that

Calculating the inverse function

Remember that inverse function “undoes” the effect of the original function. That is, solve for $x$ in $y = f(x)$. You can either solve for $x$ then switch $x$ and $y$, or you can switch first then solve for $y$; it is personal preference which order you do it in.

Example: Find $f^{-1}(x)$ given that

$$f(x) = \frac{(3x+1)(x-1)}{2x-2}$$

---

It can be shown that

$$y = f(x) = \frac{3x+1}2, \;\; x\neq1$$

which is much easier to work with. Let’s switch variables and solve for $y$.

$$\begin{align*} x &= \frac{3y+1}2, \;\; y\neq1 \\ 2x &= 3y + 1 \\ 2x - 1 &= 3y \\ \frac{2x-1}3 &= y \end{align*}$$

Note that in the original function, the point $(1, 2)$ is not part of the graph, so $(2, 1)$ is not part of the graph of $f^{-1}$.

Our final answer is

$$f^{-1}(x) = \frac{2x-1}3, \;\; x\neq2 \qed$$

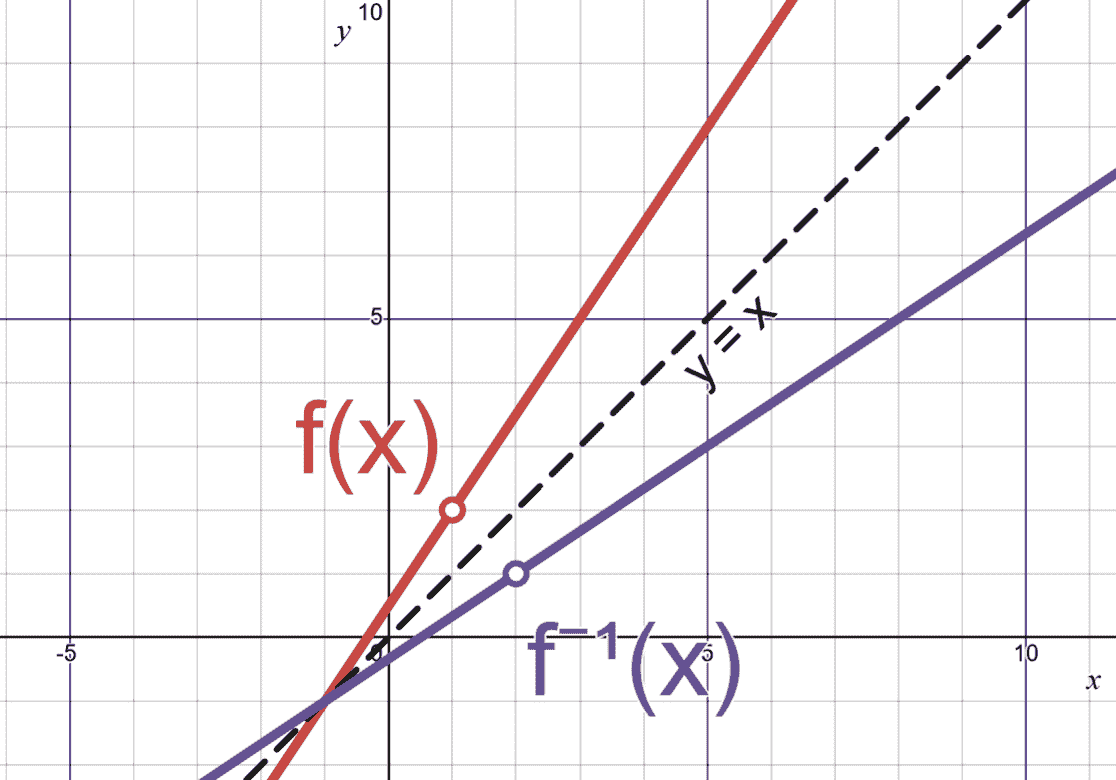
In SL, when ask to find the inverse function, the given function will be invertible. This is not necessarily the case in HL. See next page for additional steps HL candidates should do.

Calculator

Graph inverse relations on TI-84 Plus and this is not inverse functions on TI-84 Plus