Linear over linear rational functions

They look nothing like linear equations, but surprisingly $f(x) = k$ is solved in the same way.

Contents

• Graphing
• Alternative form
• Connection: derivative using quotient rule.
• Self-inverse

Graphing

It’s easier to remember if you think about how to generally find this value, rather than memorize these 4 equations with their signs.

The vertical asymptote is when denominator would be $0$:

Horizontal asymptote at large $x$, which is when $b$ and $d$ become negligible.

The $y$-intercept is when $x = 0$

The $x$-intercept is when $f(x) = 0$, ie when numerator is $0$.

See this Desmos playground  to visualize the effects of these four parameters on the shape of the graph.

The two parts of a linear over linear rational functions (as long as the linear functions are not multiples of each other), always occupy opposite corners of the asymptotes, and are rotationally symmetric about the intersection point of the asymptotes.

Example: Graph

$$f(x) = \frac{3x - 7}{2x - 4}$$

showing the asymptotes and intercepts with the axes.

---

The vertical asymptote is where denominator is zero. $x = 2$.

The $x$-intercept is where numerator is zero. $x_{\text{int}} = \frac{7}{3}$.

The horizontal asymptote is ratio of leading coefficients. $y = \frac{3}{2}$.

The $y$-intercept is $f(0) = y_{\text{int}} = \frac{7}{4}$.

By using the points $\displaystyle \left(\frac73, 0\right), {\left(0, \frac74\right)}$, we can identify which quadrants the graph lies in.

Putting it all together we obtain this graph.

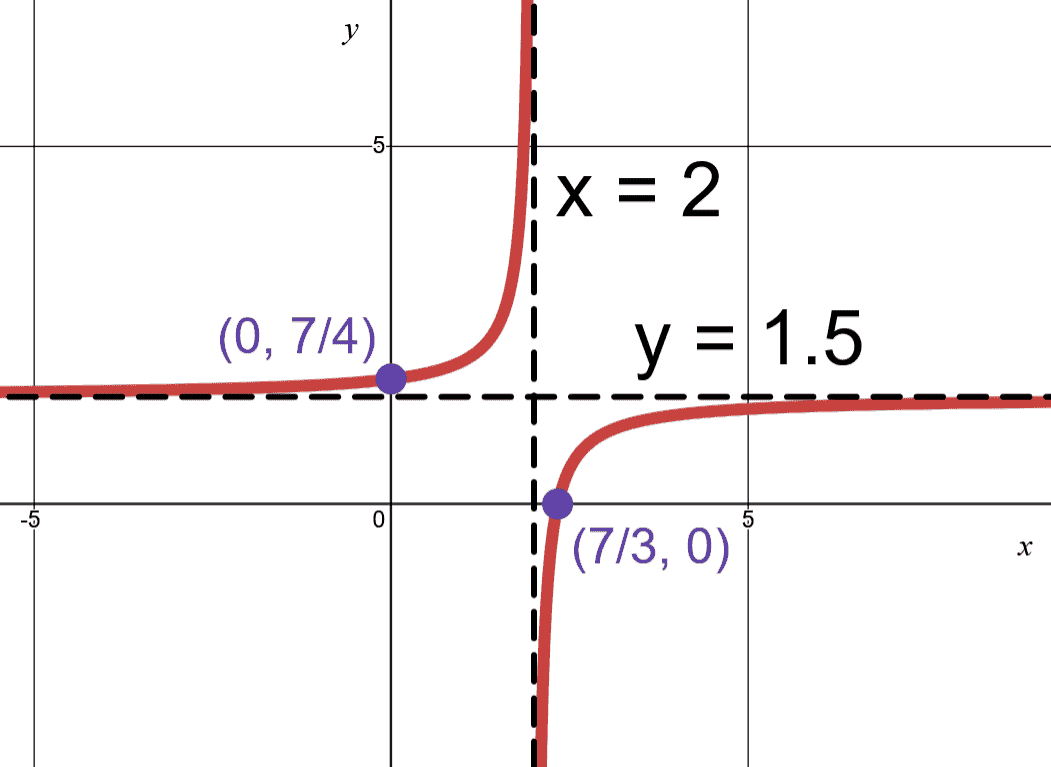
Alternative form

It can be verified that $\displaystyle \frac{6x - 4}{2x + 3} = 3 - \frac{13}{2x + 3}$, this section is about how to obtain that and how it is helpful.

In working backwards, by first finding the common denominator, we see that

In particular, using functions transformations to analyze $\displaystyle 3 - \frac{13}{2x + 3} = 3 - \frac{13}{2\left(x + \frac{3}{2}\right)}$ indicates that the horizontal asymptote is moved to $y = 3$ and vertical asymptote is moved to $x = -\frac{3}{2}$. The minus sign indicates a reflection across either $x$- or $y$-axis.

In general,

If $-ad + bc > 0$, then the rational function occupies the top-right and bottom-left corners of the asymptotes; if $-ad + bc < 0$, then it occupies the top-left and bottom-right corners.

See example using this manipulation to integrate linear over linear rational functions.

This form also slightly simplifies finding inverse functions, and solving

Connection: derivative using quotient rule.

Note that $\frac1x$ has negative derivative for all $x$, while $-\frac1x$, ie with a reflection, has positive derivative for all $x$.

From quotient rule

The denominator is always positive, so $ad - bc < 0$ means top-right and bottom-left corners of the asymptotes; $ad - bc > 0$ means top-left and bottom-right corners of the asymptotes. This matches the criterion derived from writing the function above.

Self-inverse

$\displaystyle x \mapsto \frac{ax + b}{cx - a}$ is its own inverse function. Here the horizontal asymptote is $y = \frac ac$ and the vertical asymptote is $x = \frac ac$, which allows the asymptotes and the rest of the functions to be symmetric across the $y = x$ diagonal line. Other examples of self-inverse functions are discussed at HL.