More rational functions (HL)
Contents
Common features
Vertical asymptotes are where the denominator is .
The -intercept is when .
The -intercept is when , ie when numerator is .
Linear over quadratic
See also integration of rational functions (HL)
(Not using because apparently some 18th century dude called dibs for all eternity.)
This has a horizontal asymptote , which may be crossed.
If the numerator is a factor of the denominator, then this simplifies to a reciprocal of a linear function.
This will have zero, one, or two vertical asymptotes, depending on the discriminant () of the denominator. When there is no vertical asymptote, the graph will be continuous. The graphs on both sides of a vertical asymptote may both approach , both approach or go in opposite directions, which depends on whether the discriminant of the denominator is or positive.
We’ll take a quick like at the cases. You are not expected to memorize these cases, but have a general idea of their existence.
| function | graph | notes | |
|---|---|---|---|
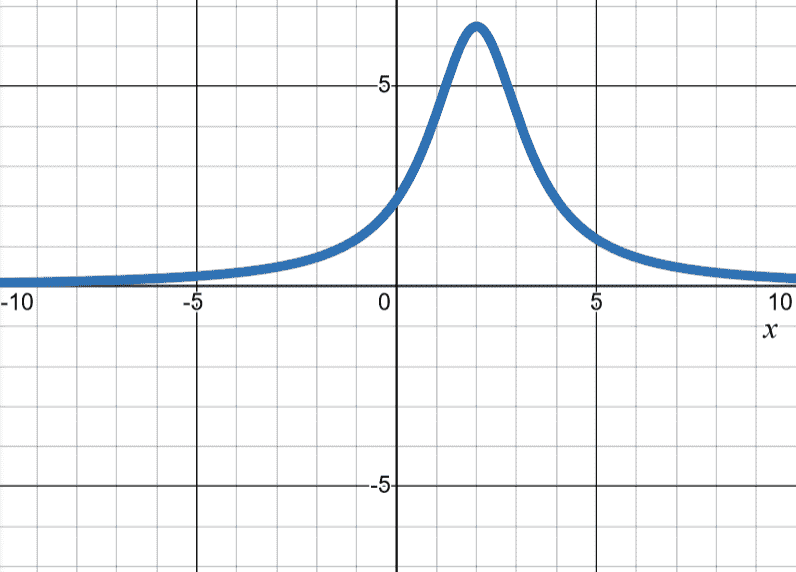 | no -intercept | ||
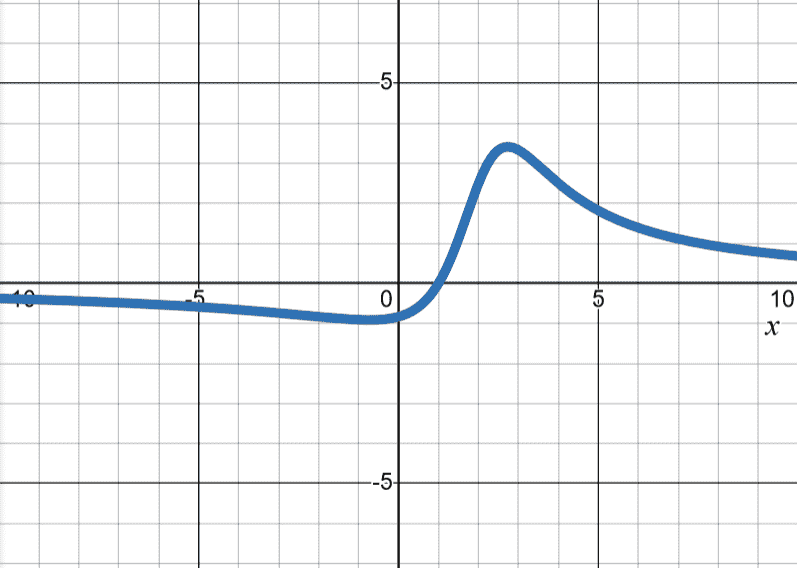 | has -intercept local max, local min | ||
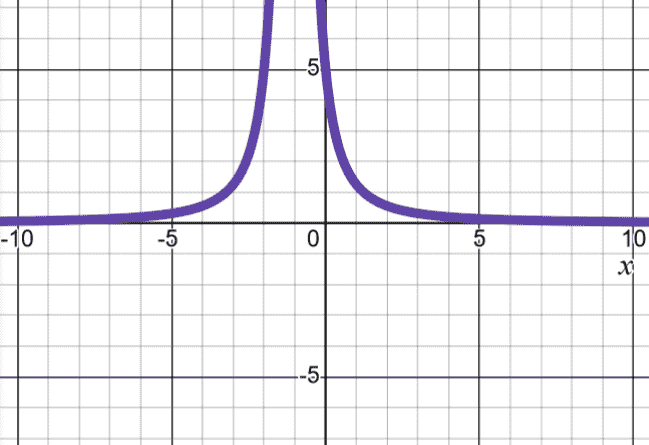 | no -intercept | ||
 | has -intercept and local extremum | ||
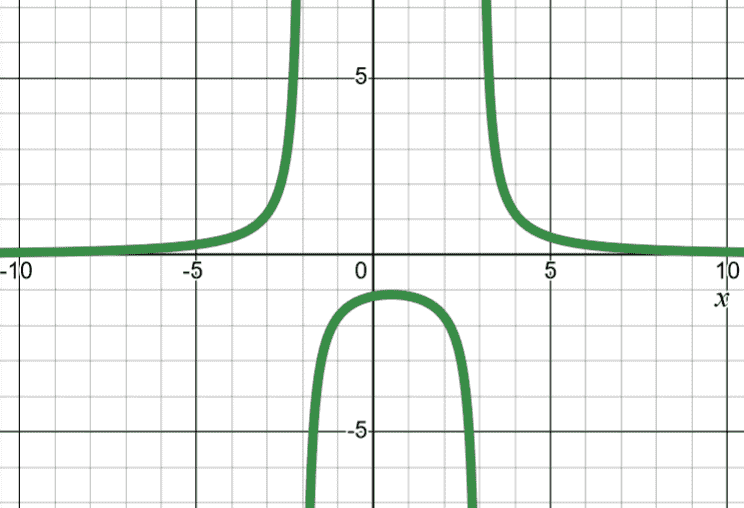 | no -intercept | ||
 | -intercept between two asymptotes | ||
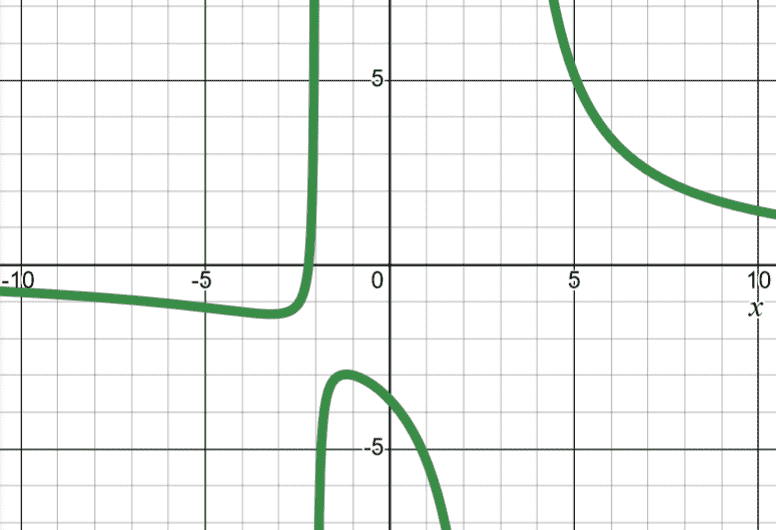 | -intercept outside two asymptotes, has two local extrema |
When the -intercept is very close to one of the asymptotes, the graph becomes more skewed. It was done so in the last example to highlight the existence of two local extrema.
Quadratic over linear
If the denominator is a factor of the numerator, this becomes a linear function with a hole at .
Otherwise, there is an oblique (diagonal) asymptote that can be found using polynomial division. If the asymptote exists, the function may be written as
with being the oblique asymptote. makes the graph roughly in the first and third quadrants, and makes it in the second and fourth quadrants, similar to albeit with different curvature due to the non-perpendicular asymptotes.
| function | graph | notes |
|---|---|---|
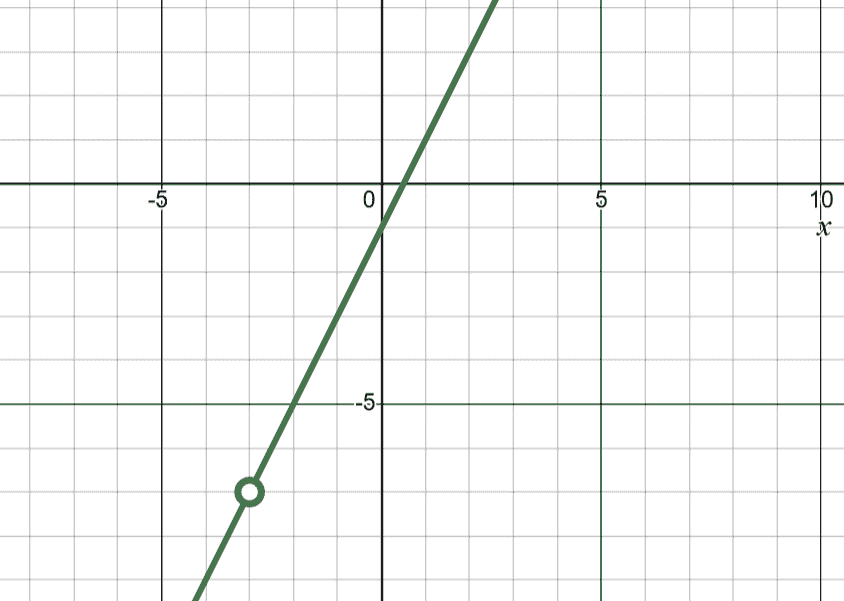 | , hole, when denominator is a factor of the numerator | |
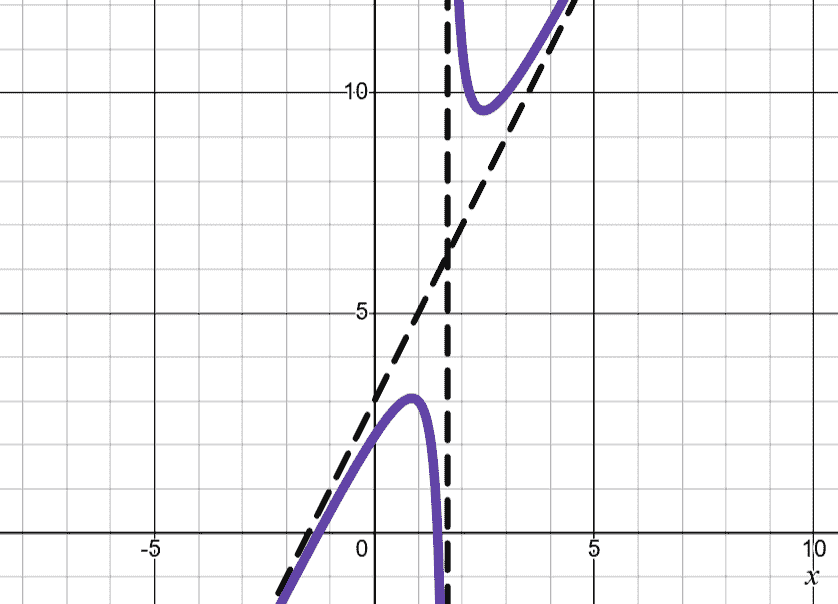 | , top right and bottom left of the asymp. | |
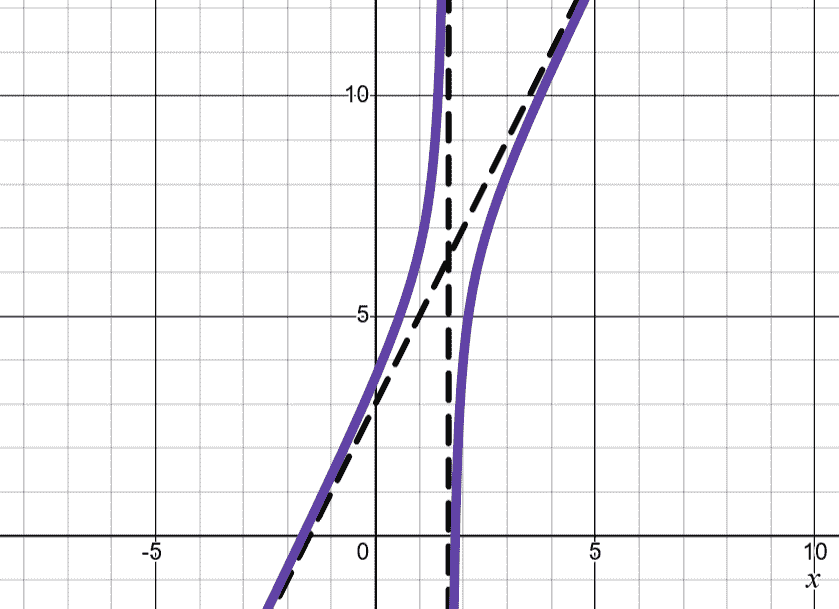 | , top left and bottom right of the asymp. |
Note that at a vertical asymptote, one side will approach and the other . This is different from dividing by some in the case of linear over quadratic, which allows both sides to approach or . Also, unlike linear over quadratic, the number of zeros do not appreciably affect the overall shape.
Check your understanding
Finding complete answers to some of these questions may require tinkering beyond what is discussed above.
For rational functions in the form of linear over quadratic
- What is the horizontal asymptote?
- When does the function intersect the horizontal asymptote?
- How to find equation(s) for the vertical asymptote(s)?
- In cases with at least one vertical asymptote, the function on either side could either both approach positive (or negative) infinity, or one approach and the other . Describe a foolproof method to deduce which case it is.
- How does the ratio of the leading terms of the numerator and denominator indicate the shape of the function at very positive and very negative values?
Use your answers to sketch the following functions, showing the asymptotes, - and -intercepts, along with the general correct shape.
For rational functions in the form of quadratic over linear,
- Explain how is a different function than .
- Suppose such a function has two asymptotes. Write down equation of the vertical asymptote, and the gradient (slope) of the oblique asymptote.
- What is the domain? Explain how the different cases produce different ranges.
- Outline why such functions have either zero or two local extrema. Point to specifics in the general equation that prevents the graph from having exactly one local extremum.
- Suppose a vertical asymptote exists, describe the behavior of the graph near the asymptote. Explain when and why the behavior is occasionally different for vertical asymptote in linear over quadratic rational functions.
Use your answers to sketch the following functions, state the asymptotes, - and -intercepts, along with the general correct shape.
Extension
See also reciprocal of functions (HL)