Right triangle trigonometry in 2D and 3D

The entirety of trigonometry is based on similarity and right triangles.

Contents

• Trigonometric ratios
• Inverse trigonometric functions
• Applications
  • definitions
  • angle between two lines in 3D
  • angle between a line and a flat surface
  • angle between two flat surfaces
  • strategies
• See also

Trigonometric ratios

For an acute angle $\theta$ in a right triangle, we define

as ratios of side lengths in a right triangle.

For similar triangles, $\sin\theta$, $\cos\theta$, and $\tan\theta$ remain the same, despite changes in side lengths. In other words, the trigonometric ratios only depend on the angle, so they are also called trigonometric functions.

In right triangles, trig ratios are useful when you need to find a missing side.

To find the angle, use the $\arcsin$, $\arccos$, and $\arctan$ functions of the ratio of the sides.

Example: Using a diagram or otherwise, simplify

$$\arctan\frac{1+\cos\theta}{\sin\theta},\,0 < \theta \leq \frac\pi2$$

---

From the Pythagorean identity, we have

$$\sin^2\theta + \cos^2\theta = 1$$

which corresponds to a right triangle ${ABC}$ with ${\theta = A\hat{C}B}$ and legs ${AB = \sin\theta}$, ${BC = \cos\theta}$, and hypotenuse $AC = 1$. ${1+\cos\theta}$ can be interpreted as the base of a larger triangle $ABD$ while keeping the height of $\sin\theta$. Here is a diagram.

From sum of angles in triangle $ABC$, we have $B\hat{A}C = 90\degree - \theta.$

From supplementary angles and sum of angles in triangle $ACD$, we have $\theta = C\hat{A}D + C\hat{D}A$

Since $AC = AD = 1$, triangle $ACD$ is isosceles, meaning the two remaining angles are equal and must be $\frac{\theta}{2}$. Here is a diagram with all the new information as well.

Then by definition of $\tan$, the desired angle is $B\hat{A}D$ with opposite side $1 + \cos \theta$ and adjacent $\sin\theta$.

$$\begin{align*} \arctan\frac{1+\cos\theta}{\sin\theta} &= 90\degree - \theta + \frac{\theta}2 \\ &= 90\degree - \frac{\theta}2 \qed \end{align*}$$

Inverse trigonometric functions

Inverse trig functions $\sin^{-1}(x)$, $\cos^{-1}(x)$, $\tan^{-1}(x)$ return the angle when you have the ratio $x$. They are useful for missing angles.

Applications

definitions

The angle of elevation is the angle from horizontal up to some point of interest. The angle of depression is the angle from horizontal down to some point of interest.

angle between two lines in 3D

This does not require special consideration, other than that you should use the plane containing the angle, then find the angle as usual.

angle between a line and a flat surface

Use a second surface that is perpendicular to the first surface and containing the line in equestion. The angle is the angle between the line and the intersection line.

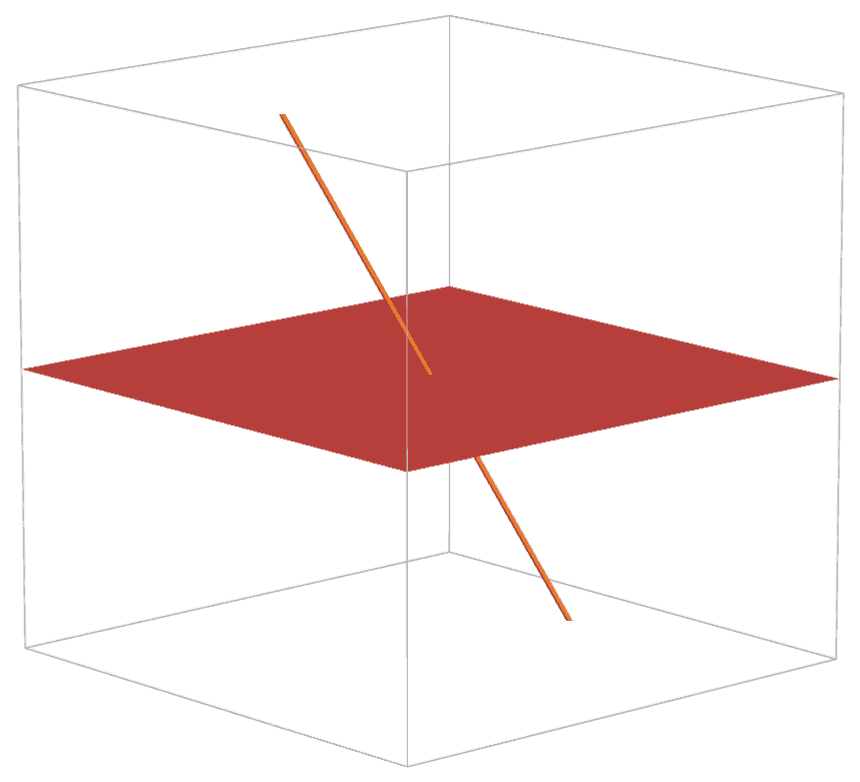
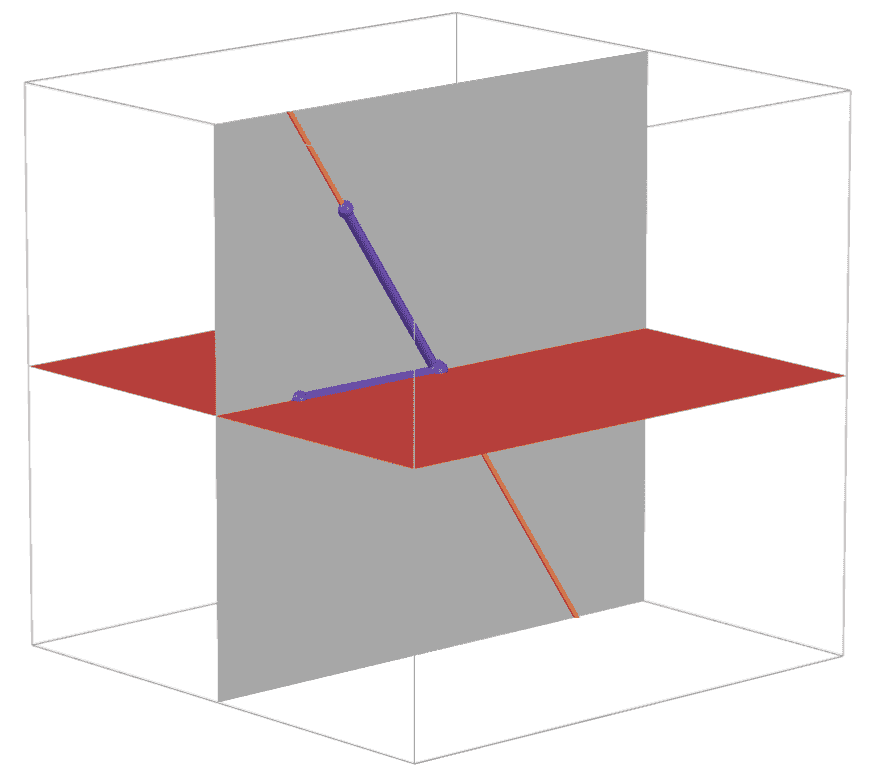
angle between two flat surfaces

You need to find a third surface perpendicular to both surfaces. This new surface intersects either surface at straight lines. The angle between the two flat surfaces is the angle between the two lines.

Open surface-surface illustration with Desmos 

See angles using vectors for advanced angle-finding using vectors (HL).

strategies

• Draw a diagram, label important points and given angles and sides (distances).
• Light travels in a straight line.
• Identify right angles.
• Identify similar triangles.
• Reuse variables when possible. For example if total distance is $10$, you can label part of it $x$ and the remaining $10 - x$.
• Verify your calculator is in degrees mode, when working with angles in degrees.

See also

For exact trigonometric ratios that you should remember, see Exact ratios