Intersection of 3 planes (HL)

We shall visualize a system of 3-variable linear equations as the intersection of 3 planes.

Contents

Vectors refresher

Geometrically, 3x−y+2z=53x - y + 2z = 5 is a plane or infinite flat surface. (3,−1,2)(3, -1, 2) is the direction that the plane faces, and is called the normal vector. The 55 specifies the particular plane out of the infinitely many parallel planes. For example, 3x−y+2z=43x - y + 2z = 4 would be a parallel plane.

−9x+3y−6z=−15-9x + 3y - 6z = -15 is the same (identical) plane as 3x−y+2z=53x - y + 2z = 5, as we just multiplied the equation by −3-3.

Two planes could either be identical, parallel, or intersecting. The intersecting line is perpendicular to both normal vectors.

Cases

When two planes are identical, the third plane could be also identical, parallel, or intersecting. This simplifies to intersection of 2 planes.

When (at least) two planes are parallel, theres is no solution.

Note: Before solving a problem, confirm that the three normal vectors are not scalar multiples of each other.

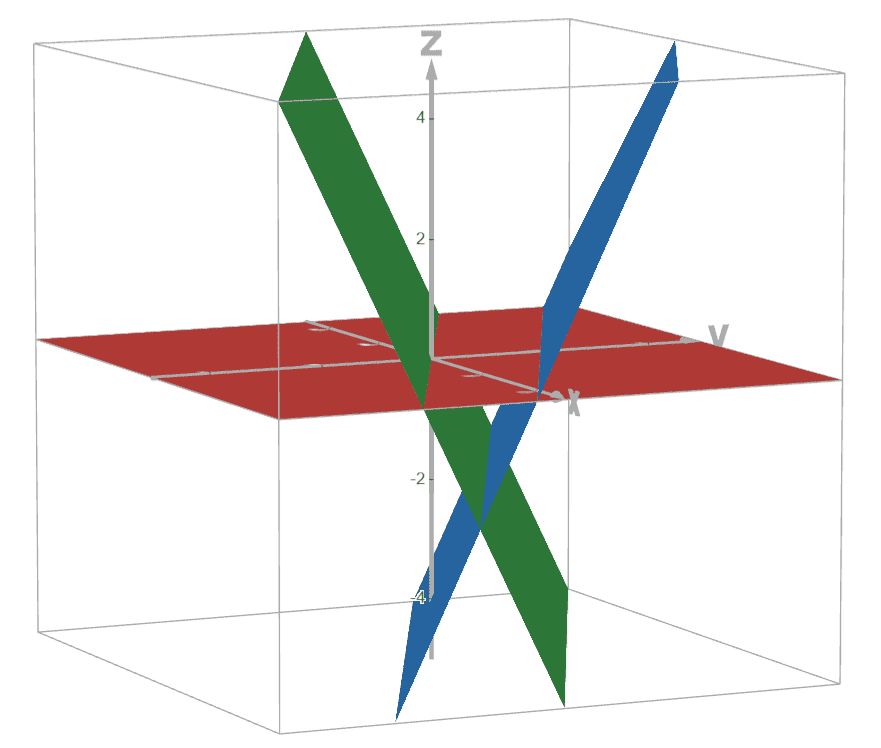
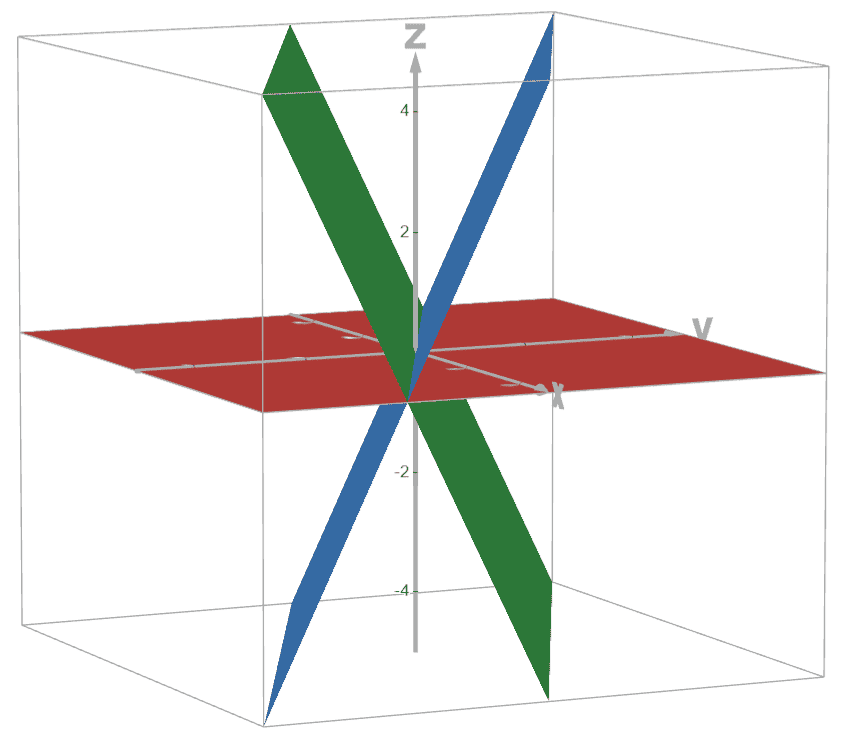
Finally, the three non-parallel planes could intersect at a point, intersect at a line, or do not intersect at all.

Suppose 3x−y+2z=53x - y + 2z = 5 is one of three planes that meet at a line. If the 55 is switched to any other number then there is an infinite family of no intersection.

Likewise, if any component of the normal vector is changed, such as from (3,−1,2)(3, -1, 2) to (3,0,2)(3, 0, 2), while remaining non-parallel to the two remaining normal vectors, the three planes would instead meet at a point.

We present two methods, extensions from the two methods presented in intersection of two planes.

Method using scalar triple product

This method assume knowledge of scalar triple product and equations of lines

The scalar triple product (a⃗×b⃗)⋅c⃗(\vec a \times \vec b)\cdot \vec c produces a scalar value, whose absolute value is the volume of the parallelepiped (a skewed rectangular prism) spanned by the three vectors.

When the scalar triple product of the three normal vectors of the three planes is 00, the three normals are coplanar, meaning the system has no or an infinite number of solutions. If it is non-zero, there is a unique solution.

Example: Find kk and mm such that the system has an infinite number of solutions.

x+ky+2z=−112x−8y+3z=m3x−y+5z=−7\begin{align*} x + ky + 2z &= -11 \\ 2x - 8y + 3z &= m \\ 3x -y + 5z &= -7 \\ \end{align*}

The scalar triple product can be evaluated in any order, but it may be off by a negative sign. Since we just want to set it to 0, the order does not matter. Because cross product is harder, we do it first with the known normals.

(2,−8,3)×(3,−1,5)=(−37,−1,22)=d(2, -8, 3) \times (3, -1, 5) = (-37, -1, 22) = \bm d

Now set the dot product between this and the remaining normal, to 0.

−37(1)−1(k)+22(2)=0k=7■\begin{align*}-37(1) -1(k) + 22(2) &= 0 \\ k &= 7 \qed \end{align*}

Because the line is perpendicular to all three normals, its direction vector is (−37,−1,22)(-37, {\color{green}-1}, 22).

To find a point P(x0,y0,z0)P(x_0, y_0, z_0) on this line, we take the component of d\bm d that is closest to 0 (but is not 0){\color{green}\text{closest to 0 (but is not 0)}} and set the corresponding component of PP to an arbitrary value{\color{blue}\text{arbitrary value}}. Let’s say y0=0{\color{green}y_0} = {\color{blue}0}.

Tip: Because dy=−1\bm d_y = -1, setting y0=0y_0 = 0 ensures integer components for the point. If we had set z0=0z_0 = 0, we’d have a 2122\frac{21}{22} chance of having to working with fractions.

Note: If a component of d\bm d is 00, do not guess the corresponding component of the point.

To find x0x_0 and y0y_0, we solve a system of equations using our two known planes at this point. Subscripts are used for clarity. You do not need to use subscripts in your solutions.

x0+7y0+2z0=−113x0−y0+5z0=−7\begin{align*}x_0 + 7y_0 + 2z_0 &= -11 \\ 3x_0 - y_0 + 5z_0 &= -7 \end{align*}

and our guess of y0=0y_0 = 0 simplifies the system down to

x0+2z0=−113x0+5z0=−7\begin{align*}x_0 + 2z_0 &= -11 \\ 3x_0 + 5z_0 &= -7 \end{align*}
x0=41,z0=−26x_0 = 41, z_0 = -26

The point (41,0−26)(41, 0 -26) is a solution and is on all three planes.

So it is on 2x−8y+3z=m2x - 8y + 3z = m.

2(41)−8(0)+3(−26)=m=4■2(41) - 8(0) + 3(-26) = m = 4 \qed

The planes intersect at r⃗=(−37,−1,22)t+(41,0,−26)\vec r = (-37, -1, 22)t + (41, 0, -26).

Tip: There would be exactly one solution for k≠7k\neq 7 and no solutions for k=7,m≠4k = 7, m \neq 4.

The actual solution was found via finding intersection of two planes, for which we already have the direction vector. The scalar triple product is only useful in finding the missing coefficient, and is not needed when coefficients are all given.

The example above told us about a line of solution. Had we not known that, we would have to find the intersection between the line and the third plane, for which there can be zero, exactly one, or an infinite number of intersections.

Method using row reduction

Using row operations is another reliable method. Each elementary row operation uses the rows from the previous step.

In the reduced echelon form, the last row tells us about number of solutions. See intersection of two planes#row reduction for row reduction rules.

example interpretation number of solutions
0 0 0 ∣ 10\,0\,0\, \vert\, 1 0=10 = 1 no solutions
0 0 1 ∣ 60\,0\,1\, \vert\, 6 z=6z = 6 one solution
0 0 0 ∣ 00\,0\,0\, \vert\, 0 0=00 = 0 infinite number of solutions

Example: Find kk and mm such that the system has an infinite number of solutions.

x+ky+2z=−112x−8y+3z=m3x−y+5z=−7\begin{align*} x + ky + 2z &= -11 \\ 2x - 8y + 3z &= m \\ 3x -y + 5z &= -7 \\ \end{align*}

The system can be represented as an augmented matrix.

[1k2−112−83m3−15−7]\left[\begin{array}{ccc|c} 1 & k & 2 & -11 \\ 2 & -8 & {\color{blue}3} & m \\ {\color{purple}3} & -1 & 5 & -7 \end{array}\right]

The goal, for this question, is to get the first row to look like

0f(k)0g(m)\begin{array}{ccc|c} 0 & f(k) & 0 & g(m) \end{array}

where f(k)f(k) and g(m)g(m) are functions (expressions) of kk and mm respectively, using some row reduction

R1+aR2+bR3→R1R_1 + aR_2 + bR_3 \to R_1

By inspection, this can be done by R1+R2−R3→R1R_1 + R_2 - R_3 \to R_1.

For more complex situation, you may need to solve a system of two-variable equations, such as

2a+3b=−13a+5b=−2\begin{align*} 2a + {\color{purple}3}b &= -1 \\ {\color{blue}3}a + 5b &= -2 \\ \end{align*}

for the multipliers aa and bb that cancel out the 11 and 22 in the first equation. Here we obtain

a=1b=−1\begin{align*} a &= 1 \\ b &= -1 \\ \end{align*}

Then in a single step

R1+R2−R3→R1[0k−70−4+m2−83m3−15−7]R_1 + R_2 - R_3 \to R_1 \\ \left[\begin{array}{ccc|c} 0 & k - 7 & 0 & -4 + m \\ 2 & -8 & 3 & m \\ 3 & -1 & 5 & -7 \end{array}\right]

There are infinite solutions when we have a row of all zeros

0000\begin{array}{ccc|c} 0 & 0 & 0 & 0 \end{array}

and that happens at k=7,m=4■k = 7, m = 4 \qed

To actually find the solutions, row reductions need to be done in full, reaching the row echelon form for zero or infinite solutions, and the row-reduced echelon form for exactly one solution.

The row echelon form looks like

[ABCD0EFG00HI]\begin{align*} \left[\begin{array}{ccc|c} A & B & C & D \\ 0 & E & F & G \\ 0 & 0 & H & I \\ \end{array}\right] \end{align*}

Though ideally you want it in the form of

[10CD01FG00HI]\begin{align*} \left[\begin{array}{ccc|c} 1 & 0 & C & D \\ 0 & 1 & F & G \\ 0 & 0 & H & I \\ \end{array}\right] \end{align*}

where at least two columns on the left have at most one one and rest zeros. This above matrix is interpreted as

x+Cz=Dy+Fz=GHz=I\begin{align*} x + Cz = D \\ y + Fz = G \\ Hz = I \end{align*}

Example: Solve

x+7y+2z=−112x−8y+3z=43x−y+5z=−7\begin{align*} x + 7y + 2z &= -11 \\ 2x - 8y + 3z &= 4 \\ 3x -y + 5z &= -7 \\ \end{align*}

The system can be represented as an augmented matrix.

[172−112−8343−15−7]\left[\begin{array}{ccc|c} 1 & 7 & 2 & -11 \\ 2 & -8 & 3 & 4 \\ 3 & -1 & 5 & -7 \end{array}\right]

Subtract the second equation by twice the first, and subtract the third equation by thrice the first.

R2−2R1→R2R3−3R1→R3[172−110−22−1260−22−126]R_2 - 2R_1 \to R_2 \\ R_3 - 3R_1 \to R_3 \\ \left[\begin{array}{ccc|c} 1 & 7 & 2 & -11 \\ 0 & -22 & -1 & 26 \\ 0 & -22 & -1 & 26 \end{array}\right]

Tip: Typically we proceed by making second column (the yy’s) second row contain only a 1, but it’s much easier here to make third column to only contain a 1.

R1+2R2→R1−R2→R2R3−R2→R3[1−370410221−260000]R_1 + 2R_2 \to R_1\\ -R_2 \to R_2\\ R_3 - R_2 \to R_3\\ \left[\begin{array}{ccc|c} 1 & -37 & 0 & 41 \\ 0 & 22 & 1 & -26 \\ 0 & 0 & 0 & 0 \end{array}\right]

A row of all zeros means a line of solutions. An empty row with a non-zero value on the right means no solution.

The equivalent equations are

x−37y=4122y+z=−26\begin{align*} x - 37y &= 41 \\ 22y + z &= -26 \\ \end{align*}

let t=yt = y, as yy is common to both equations. The goal is to reduce down to a consistent system of two equations.

Assume a point whose yy component is 00.

x=37t+41y=tz=−22t−26■\begin{align*} x &= 37t + 41 \\ y &= t \\ z &= -22t - 26 \qed \\ \end{align*}

These are a set of parametric equations for the line of solutions.

In summary, the method of row reductions is often easier and more systematic. It is the recommended approach according to IB. The only time scalar triple product can be faster is when you need to solve for two coefficients and find the solution(s), which is pretty much never.

Incorrect methods

Method such as inverse matrices or Cramer’s rule are inappropriate for AA HL, because they only work for 3-variable systems with a unique solution. That’s like trying to solve all quadratics by factoring.

Calculators

This page focuses on Paper 1, ie solving by hand. When all coefficients are known, this could also be solved on calculators. For example on TI-84 Plus, use the PolySmlt App allowed on exams. On others without a dedicated app, you may use the rref matrix operator, but most will have an app.

Previous HL:
Next HL: